Gauss Jordan

Eliminasi Gauss Jordan.

Sejarah:

Karl Friedich Gauss (1977-1855) adalah seorang ahli matematika dan ilmuwan dari Jerman. Gauss yang kadang-kadang dijuluki "pangeran ahli matematika". Disejajarkan dengan Isaac Newton dan Archimedes sebagai salah satu dari tiga ahli matematika yang terbesar yang pernah ada. Dalam seluruh sejarah matematika, tidak pernah ada seorang anak yang begitu cepat berkembang, sebagaimana Gauss, yang dengan usahanya sendiri menyelesaikan dasar aritmetika sebelum ia dapat berbicara. Pada suatu hari, saat ia bahkan belum berusia tiga tahun, melalui cara dramatis orang tuanya mulai menyadari kejeniusan Gauss. Ketika itu ayahnya tengah menyiapkan gaji mingguan untuk para buruh bawahannya, dan Gauss memperhatikan dengan diam-diam dari pojok ruangan. Setelah perhitungan yang panjang dan membosankan. Gauss tiba-tiba member tahu ayahnya bahwa terdapat kesalahan dalam perhitungannya dan memberikan jawaban yang benar, yang diperoleh hanya dengan memikirkannya (tanpa menulisnya). Yang mengherankan orang tuanya adalah setelah diperiksa ternyata perhitungannya Gauss benar!

Dalam desertasi doktoralnya Gauss memberikan bukti lengkap pertama teori-teori dasar aljabar yang menyatakan bahwa setiap persamaan polynomial memiliki solusi sebanyak pangkatnya. Pada usia 19 tahun ia menyelesaikan masalah yang membingungkan Euclid, menggambarkan polygon 17 sisi di dalam lingkaran dengan menggunakan jangka dan kompas, dan pada tahun 1801, pada usia yang ke-24 tahun, ia mempublikasikan karya terbesarnya, Disquisitiones Arithmeticae", yang dipandang banyak orang sebagai salah satu prestasi paling berlian dalam matematika. Dalam makalah itu Gauss melakukan sistematisasi studi dari teori bilangan (sifat-sifat bilangan bulat atau integer) dan merumuskan konse dasar dari hal tersebut.

Diantara prestasinya yang banyak sekali, Gauss menemukan kurva Gaussian atau kurva berbentuk lonceng yang merupakan dasar teori probabilitas, memberikan interpretasi geometric pertama mengenai bilangan kompleks dan mengembangkan metode-metode karakteristik permukaan secara interistik dengan menggunakan kurva-kurva yang dikandungnya, mengembangkan teori pemetaan konformal (angle preserving) dan menemukan geometri non-Euclidean 30 tahun sebelum dipublikasikan oleh orang lain. Dalam bidang fisika ia memberikan sumbangan yang besar terhadap teori lensa dan gerakan kapiler, dan bersama Wilhelm Weber ia mengerjakan pekerjaan penting dalam bidang elektromagnetisme, magnetometer bifilar dan elektrograf.Gauss adalah orang yang sangat religious dan aristoratik dalam kesajaannya. Ia dengan mudah menguasai bahasa-bahasa asing, sangat senang membaca dan meminati bidang minarologi dan botani sebagai hobi. Ia tidak suka mengajar dan biasanya bersikap dingin tidak mendukung terhadapahli matematika yang lainnya, kemungkinan ini karena ia mengantisipasi kerja mereka. Dikatakan bahwa jika saja Gauss mempublikasikan semua penemuaannya, maka matematika saat ini akan lebih maju 50 tahun. Tak diragukan lagi bahwa ia adalah ahli matematika terbesar dalam era modern.

Wilhelm Jordan (1842-1899) adalah seorang insinyur Jerman yang ahli dalam bidang geodesi. Sumbangannya untuk penyelesaian sistem linear dalam buku populernya, Handbuch de Vermessungskunde (Buku panduan Geodesi) pada tahun 1988.

Contoh Sumbangannya untuk penyelesaian sistem linear dalam buku populernya

Dalam aljabar linear, eliminasi Gauss-Jordan adalah versi dari eliminasi Gauss. Pada metode eliminasi Gauus-Jordan kita membuat nol elemen-elemen di bawah maupun di atas diagonal utama suatu matriks. Hasilnya adalah matriks tereduksi yang berupa matriks diagonal satuan (Semua elemen pada diagonal utama bernilai 1, elemen-elemen lainnya nol).

Metode eliminasi Gauss-Jordan kurang efisien untuk menyelesaikan sebuah SPL, tetapi lebih efisien daripada eliminasi Gauss jika kita ingin menyelesaikan SPL dengan matriks koefisien sama.

Motede tersebut dinamai Eliminasi Gauss-Jordan untuk menghormati Carl Friedrich Gauss dan Whilhelm Jordan.

Aplikasi untuk mencari InversJika eliminasi Gauss-Jordan diterapkan dalam matriks persegi, metode tersebut dapat digunakan untuk menghitung invers dari matriks. Eliminasi Gauss-Jordan hanya dapat dilakukan dengan menambahkan dengan matriks identitas dengan dimensi yang sama, dan melalui operasi-operasi matriks:

Jika A contoh matriks persegi yang diberikan:

Kemudian, setelah ditambahkan dengan matriks identitas:

Dengan melakukan operasi baris dasar pada matriks[AI] sampai A menjadi matriks identitas, maka didapatkan hasil akhir:

Eliminasi Gauss-Jordan

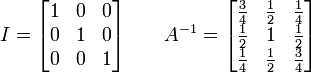
Thomas (1984:93-94) mengatakan bahwa setiap matriks memiliki bentuk eselon baris tereduksi yang unik, artinya kita akan memperoleh bentuk eselon baris tereduksi yang sama untuk matriks tertentu bagaimanapun variasi operasi baris yang dilakukan.

Langkah-langkah operasi baris yang dikemukakan oleh Gauss dan disempurnakan oleh Jordan sehingga dikenal dengan Eliminasi Gauss-Jordan, sebagai berikut:

Jika suatu baris tidak seluruhnya dari nol, maka bilangan tak nol pertama pada baris itu adalah

1. Bilangan ini disebut 1 utama (leading 1).
2. Jika terdapat baris yang seluruhnya terdiri dari nol, maka baris-baris ini akan dikelompokkan bersama pada bagian paling bawah dari matriks.
   
3. Jika terdapat dua baris berurutan yang tidak seluruhnya dari nol, maka 1 utama pada baris yang lebih rendah terdapat pada kolom yang lebih kanan dari 1 utama pada baris yang lebih tinggi.
4. Setiap kolom memiliki 1 utama memiliki nol pada tempat lain.

Misal kita punya matriks berikut:

Langkah 1. Perhatikan kolom paling kiri yang tidak seluruhnya nol.

Langkah 2. Jika perlu, pertukarkan baris paling atas dengan baris lain untuk menempatkan entri taknol pada puncak kolom yang kita peroleh pada langkah 1.

Baris pertama dipertukarkan dengan baris ke dua (H21)

Langkah 3. Jika entri yang kini berada pada kolom yang kita peroleh pada langkah 1 adalah a, kalikan dengan baris pertama dengan 1/a sehingga membentuk 1 utama.

Baris pertama dari matriks sebelumnya dikalikan dengan 1/2 disingkat H2(1/2)

Langkah 4. Tambahkan kelipatan yang sesuai dari baris paling atas ke baris-baris di bawahnya sehingga semua entri di bawah 1 utama menjadi nol.

-2 kali baris pertama sebelumnya ditambahkan ke baris ketiga (H21(-2))

Langkah 5. Sekarang tutuplah baris paling atas dari matriks dan mulailah lagi dengan langkah 1 pada submatriks yang tersisa. Lanjutkan langkah ini hingga seluruhnya matriks berada dalam bentuk eselon baris.

lihat kolom ketiga dari kiri tidak semuanya nol

baris kedua dari matriks dikalikan dengan dengan -1/2 untuk memperoleh 1 utama

-5 kali baris kedua ditambahkan pada baris ketiga untuk memperoleh nol di bawah 1 utama.

baris paling atas submatriks ditutup kita kembali ke langkah 1

baris ketiga dikalikan dengan 2 untuk mendapatkan 1 utama berikutnya.

Langkah 6. Mulailah dengan baris tak nol terakhir dan bergerak ke atas, tambahkan kelipatan yang sesuai dari tiap-tiap baris ke baris di atasnya untuk memperoleh nol di atas 1 utama.

kali baris ketiga dari matriks sebelumnya ditambahkan ke baris kedua.

-6 kali baris ketiga ditambahkan ke baris pertama

5 kali baris kedua ditambahkan ke baris pertama

Langkah 1 - 5 dinamakan Eliminasi Gauss, jika prosedurnya sampai pada langkah 6 dinamakan Eliminasi Gauss-Jordan.

Dari langkah tersebut kita peroleh persamaan

x1 + 2x2 +3 x4 = 2

x3 = 1

x5=2

Dari persamaan tersebut kita dapat memisalkan nilai x1=s dan x2 = t untuk memperoleh nilai x1 = 2s-3t (s dan t adalah parameter dari SPL tersebut).

dapat dilihat di sini Eliminasi gauss-jordan

Referensi

Lipschutz, Seymour, and Lipson, Mark. "Schaum's Outlines: Linear Algebra". Tata McGraw-hill edition. Delhi 2001. pp. 69-80.

Strang, Gilbert (2003). Introduction to Linear Algebra, 3rd edition, Wellesley, Massachusetts: Wellesley-Cambridge Press, 74-76.

Sahid. Pengantar Komputasi Numerik dengan MATLAB. 2005. Yogyakarta:ANDI